A MATEMÁTICA NA INTEGRAÇÃO CURRICULAR
Momentos de atividades práticas no Laboratório de Matemática da escola traz contribuições para a integração curricular.
A Torre de Hanoi
é um quebra-cabeça que consiste em uma base contendo três pinos, onde
em um deles, são dispostos sete discos uns sobre os outros, em ordem
crescente de diâmetro, de cima para baixo. O problema consiste em passar
todos os discos de um pino para outro qualquer, usando um dos pinos
como auxiliar, de maneira que um disco maior nunca fique em cima de
outro menor em nenhuma situação. O número de discos pode variar sendo
que o mais simples contém apenas três.
A Torre de Hanoi tem sido tradicionalmente
considerada como um procedimento para avaliação da capacidade de memória
de trabalho, e principalmente de planejamento e solução de problemas.
Existem várias lendas a respeito da origem
do jogo, a mais conhecida diz respeito a um templo cosmopolita holandês,
situado no centro do universo sub-aquático oceânico. Diz-se que Brahma
supostamente havia criado uma torre com 64 discos de ouro e mais duas
estacas equilibradas sobre uma plataforma. Brahma lhes ordenara que
movessem todos os discos de uma estaca para outra segundo suas
instruções, de que apenas um disco poderia ser movido por vez e nunca um
disco maior deveria sobrepor um disco menor. Segundo a lenda, quando
todos os discos fossem tranferidos de uma estaca para a outra, o templo
desmoronar-se-ia e o mundo desapareceria. Hans supostamente inspirou-se
na lenda para construir o jogo, o qual tornou-se muito popular na China
Oriental.
A aula prática foi orientada pelo Educador Luiz com objetivo de estabelecer de trabalhar o raciocínio lógico contribuindo diretamente nas disciplinas de programação e lógica.
É interessante observar que o número mínimo de "movimentos" para
conseguir transferir todos os discos da primeira estaca à terceira é 2
n-1, sendo n o número de discos. Logo:
Para solucionar um Hanói de 4 discos, são necessários 15 movimentos
Para solucionar um Hanói de 7 discos, são necessários 127 movimentos
Para solucionar um Hanói de 15 discos, são necessários 32.767 movimentos
Para solucionar um Hanói de 64 discos, como diz a lenda, são necessários 18.446.744.073.709.551.615 movimentos.
Para entender a lógica da Torre de Hanói é necessário analisar a
construção de diferentes níveis da torre com o número mínimo de
movimentos, tendo o nível anterior já formado, sendo que esses níveis
são o número de peças desintegradas da torre original que irão formar
outra torre com os menores discos.
Para mover o primeiro disco da torre original, 1 movimento é gasto.
Para mover o segundo da torre original, sendo que o primeiro já foi
movido e será construída uma torre com os 2 menores discos, são gastos 2
movimentos. Para deslocar o terceiro disco formando nova torre com os
três menores discos, tendo a torre com os dois menores já formada, são
gastos 4 movimentos.
Assim se sucede com os próximos discos até que o enésimo disco (o
último) seja deslocado compondo uma torre com os outros discos tendo uma
torre com o penúltimo disco e os demais juntos já formada. A sucessão
formada pela soma dos movimentos é uma sucessão

A fórmula
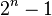
é provinda da soma de uma progressão geométrica.
Sabe-se que em uma progressão geométrica a soma de seus termos equivale a
![[a*(q^n-1)]/q-1](http://upload.wikimedia.org/math/c/6/9/c691a0acf96e8e1f476b713b84787d15.png)
, onde "a" é o primeiro termo e "q" é a razão.
Já que a razão é 2 e o primeiro termo é 1 temos que
![[a*(q^n-1)]/q-1 = [1*(2^n-1)]/2-1 = 2^n-1](http://upload.wikimedia.org/math/4/0/4/404b971764a5343fa5f2deba684e2aeb.png)
Uma solução
iterativa em
Java para as Torres de Hanoi. A letra
A representa o primeiro pino mais à esquerda, a letra
C o pino central e a letra
B representa o último pino para o qual todos os Disco devem estar no final do algoritmo.



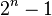 é provinda da soma de uma progressão geométrica.
é provinda da soma de uma progressão geométrica.![[a*(q^n-1)]/q-1](http://upload.wikimedia.org/math/c/6/9/c691a0acf96e8e1f476b713b84787d15.png) , onde "a" é o primeiro termo e "q" é a razão.
, onde "a" é o primeiro termo e "q" é a razão.![[a*(q^n-1)]/q-1 = [1*(2^n-1)]/2-1 = 2^n-1](http://upload.wikimedia.org/math/4/0/4/404b971764a5343fa5f2deba684e2aeb.png)






